không gian

Tuần sinh hoạt công dân của tân sinh viên năm 2020

10:54 15/10/2020

Từ ngày 12/10 đến ngày 16/10 các Tân sinh viên khóa học 2020 - 2024 của Trường Đại học Công nghiệp Quảng Ninh đã bước vào “Tuần sinh hoạt công dân - sinh viên” đầu khóa học. Đây là tuần lễ học tập bắt buộc, có ý nghĩa quan trọng đối với Tân sinh viên trước khi các em bước vào học chính thức. Sinh hoạt công dân Sinh viên đầu khóa là hoạt động thường niên Nhà trường dành cho Tân sinh viên nhằm mang đến không gian giao lưu, kết nối giữa tân sinh viên với nhà trường cũng như với các sinh viên đồng khóa và các anh chị sinh viên đi trước.

Định lý điểm bất động trong không gian H- metric

03:47 05/07/2019

Bài báo này giới thiệu và chứng minh một kiểu mới của điểm bất động cho ánh xạ đơn trị trong không gian H- Metric H- đầy đủ.

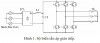
Đánh giá các phương pháp điều chế sinPWM, SVM cho biến tần gián tiếp ba pha hai bậc và biến tần trực tiếp

03:40 05/07/2019

Trong thực tế hiện nay biến tần có cấu trúc gián tiếp được dùng phổ biến vì có cấu trúc mạch lực và mạch điều khiển đơn giản, có thể sử dụng phương pháp điều chế để điều khiển các khóa bán dẫn như phương pháp điều chế độ rộng xung (PWM – Pulse Width Modulation), điều chế vector không gian (SVM – Space Vector Modulation). Với biến tần trực tiếp có nhiều loại tùy thuộc vào cấu trúc mạch lực và cấu tạo van bán dẫn (Thyristor, IGBT), trong đó có biến tần ma trận đang được nghiên cứu rộng rãi vì chúng có ưu điểm hơn so với biến tần gián tiếp là trao đổi công suất theo hai chiều, hệ số công suất cosφ có thể điều chỉnh được, chất lượng dòng điện vào và ra dạng sine. Vì vậy, việc xây dựng, lựa chọn các phương pháp điều chế cho biến tần gián tiếp và trực tiếp tùy thuộc vào ứng dụng cụ thể sẽ tiết kiệm được chi phí chế tạo, đảm bảo chất lượng làm việc của hệ thống, đồng thời đưa ra các phương pháp điều chế mới. Kết quả nghiên cứu được kiểm chứng bằng phần mềm matlab & simulink.

Phương pháp điều khiển V/F cho biến tần ma trận sử dụng điều chế véc tơ không gian trực tiếp

21:34 04/07/2019

Hiện nay các bộ biến tần ma trận (Matrix converter -MC) được coi là biến tần tiên tiến và đang được nghiên cứu rộng rãi. Đây là bộ biến tần trực tiếp AC-AC được xây dựng trên các khóa bán dẫn hai chiều với những ưu điểm nổi bật hơn so với các bộ biến đổi tần số gián tiếp có khâu trung gian một chiều (AC-DC-AC) như trao đổi công suất theo hai chiều, cho phép thực hiện hàm tái sinh năng lượng trả về lưới điện mà không cần có mạch phụ, dòng điện đầu vào có dạng sin, hệ số công suất đầu vào gần bằng 1 và có thể điều chỉnh được. Bài báo trình bày kỹ thuật điều chế véc tơ không gian trực tiếp và phương pháp điều khiển V/F ở biến tần ma trận cho động cơ xoay chiều không đồng bộ. Kết quả nghiên cứu được kiểm chứng bằng phần mềm Matlab & Simulink.

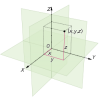
Quá trình trực chuẩn hóa Gram - Smide

20:28 01/02/2018

Không gian Euclid là một không gian vectơ n chiều được trang bị một tích vô hướng. Trong không gian Euclid, với mỗi định nghĩa tích vô hướng đưa ra thì bài toán xây dựng cơ sở trực chuẩn từ một họ véctơ cho trước là cần thiết vì các cơ sở trực chuẩn đối với không gian Euclid rất tiện lợi. Các tài liệu tham khảo thường đưa ra những công thức cồng kềnh vì phải đảm bảo về mặt kiến thức cũng như tính sư phạm. Song với sinh viên ngành kỹ thuật thì việc thực hành tính toán được quan trọng hơn việc chứng minh bản chất vấn đề .Bài viết này sẽ cụ thể hóa quá trình trực chuẩn hóa Gram - Smide.

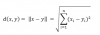
Định lý điểm bất động của ánh xạ co trong không gian sb - Metric

02:52 31/01/2018

Trong bài báo trước tôi đã giới thiệu một mở rộng của nguyên lý ánh xạ co Banach bằng cách mở rộng không gian metric thông thường sang không gian metric nón và đã chứng minh một số tính chất về hội tụ, tính liên tục, dãy Cauchy, không gian metric nón đầy đủ, đặc biệt là giới thiệu và chứng minh một số định lý điểm bất động trong không gian này. Bằng cách đó vẫn theo một trong hai hướng sau đây để xây dựng và mở rộng không gian metric và chứng minh các định lý điểm bất động trong không gian này:
(1) Thay thế điều kiện co bởi điều kiện co tổng quát hơn và xây dựng các định lý điểm bất động của ánh xạ.
(2) Thay thế không gian metric đầy đủ (X,d) bởi không gian metric tổng quát hơn.
Trong bài báo này tôi giới thiệu không gian metric, tính chất của sự hội tụ và chứng minh định lý điểm bất động trong không gian này.