định lý

Một số vấn đề về lý thuyết phân tích nguyên sơ trong Môđun

03:45 28/02/2019

Trong bài báo trước tôi đã trình bày một số vấn đề về lý thuyết phân tích nguyên sơ của iđêan, quan trọng là hai định lý duy nhất và đưa ra thuật toán tìm phân tích nguyên sơ của iđêan đơn thức. Bằng cách đó chúng tôi đã xây dựng lên phân tích nguyên sơ cho mô đun hữu hạn sinh và phân tích nguyên sơ của địa phương hóa.

Một số vấn đề về lý thuyết phân tích nguyên sơ

22:22 13/08/2018

Trong bài báo này, chúng tôi trình bày một số vấn đề về lý thuyết phân tích nguyên sơ của iđêan, quan trọng là hai định lý duy nhất và đưa ra thuật toán tìm phân tích nguyên sơ của iđêan đơn thức.

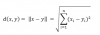
Định lý điểm bất động của ánh xạ co trong không gian sb - Metric

02:52 31/01/2018

Trong bài báo trước tôi đã giới thiệu một mở rộng của nguyên lý ánh xạ co Banach bằng cách mở rộng không gian metric thông thường sang không gian metric nón và đã chứng minh một số tính chất về hội tụ, tính liên tục, dãy Cauchy, không gian metric nón đầy đủ, đặc biệt là giới thiệu và chứng minh một số định lý điểm bất động trong không gian này. Bằng cách đó vẫn theo một trong hai hướng sau đây để xây dựng và mở rộng không gian metric và chứng minh các định lý điểm bất động trong không gian này:
(1) Thay thế điều kiện co bởi điều kiện co tổng quát hơn và xây dựng các định lý điểm bất động của ánh xạ.
(2) Thay thế không gian metric đầy đủ (X,d) bởi không gian metric tổng quát hơn.
Trong bài báo này tôi giới thiệu không gian metric, tính chất của sự hội tụ và chứng minh định lý điểm bất động trong không gian này.

Sự tồn tại và tính duy nhất nghiệm của hệ phương trình Stockes

21:43 14/12/2014

Phương trình đạo hàm riêng là một lĩnh vực rất quan trọng của toán học. Có rất nhiều mô hình trong tự nhiên được mô tả bởi các phương trình, hệ phương trình vi phân đạo hàm riêng như phương trình truyền sóng, phương trình truyền nhiêt, hệ phương trình Stokes,…. Bài báo này giới thiệu về công thức biến phân của bài toán Stokes, sự tồn tại và duy nhất nghiệm thông qua định lý phép chiếu.

Cực trị tự do của hàm nhiều biến

21:43 23/06/2014

Khi giải bài toán tìm cực trị tự do của hàm nhiều biến, sinh viên thường sử dụng định lý điều kiện đủ để hàm số có cực trị. Tuy nhiên, trong trường hợp thì sinh viên thường lúng túng vì không biết áp dụng kết quả nào. Chính vì lý do đó, tác giả bài viết đã có hướng nghiên cứu và chứng minh một số kết quả để giúp sinh viên có thể kiểm tra hàm nhiều biến (cụ thể hàm hai hai biến), có đạt cực trị tai điểm a hay không trong trường hợp